信息的二进制编码

在计算机内部，所有信息都是采用二进制进行编码和计算的，有没有想过，为什么采用这种方式？

其原因在于二进制只有两种状态，制造一个只有两个稳定状态的物理器件要比多个稳定状态的物理期间容易得多，使用高、低电位或脉冲有、无表示都很方便，能够很可靠的表示“0”和“1”。

如果都采用二进制计算，那么我们平时使用的数字、符号甚至图片和视频，都应该通过某种方式转换成二进制，
才能得以让计算机运算。这种转换方式称为“编码”。

我们人类角度看到的数据到计算机内部的数据转换如下：

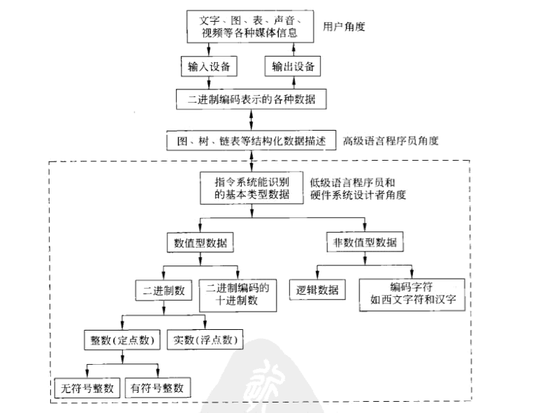
这篇文章，我们先来分析数值型数据的进制与转换规则。

进制计数制

日常生活中我们都是使用十进制数，每个数位可用10个不同符号（0-9）表示，在进行加法运算时，逢十进一。

在计算机系统中，常用的进位计数制有以下几种：

二进制R=2：基本符号为0、1
八进制R=8：基本符号为0、1、2、3、4、5、6、7
十进制R=10，基本符号为0、1、2、3、4、5、6、7、8、9
十六进制R=16，基本符号为0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F

下图列出了4种进制之间的对应关系：

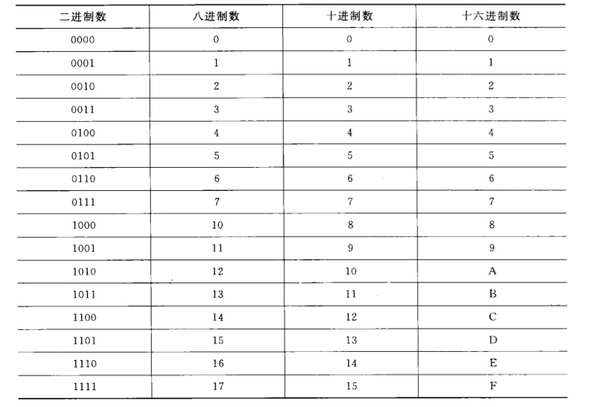
计算机内部都使用二进制编码表示，但计算机外部，我们为了书写和阅读方便，会采用八进制、十进制或十六进制。

在书写时采用后缀字母标识该数的计数制，一般用B（Binary）表示二进制，用O（Octal）表示八进制，用D（Decimal）表示十进制，用H（Hexadeciaml）表示十六进制。例如二进制10011B，十进制56D，十六进制308FH等。

那各计数制之间的数据如何转换呢？下面我们逐个进行讲解。

R进制转换成十进制

任何一个R进制数转换成十进制，只要”按权展开”即可，这个“权”就是R，我们看下面几个例子：

将二进制数10101.01转换成十进制数：

1	10101.01(B) = 1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 0 * 2^1 + 0 * 2^-1 + 1 * 2^-2 = 21.25(D)

将八进制数307.6转换成十进制数：

1	307.6(O) = 3 * 8^2 + 7 * 8^0 + 6 * 8^-1 = 199.75(D)

将十六进制数3A.C转换成十进制数：

1	3A.C(H) = 3 * 16^1 + 10 * 16^0 + 12 * 16^-1 = 58.75(D)

十进制转换成R进制

十进制转换成R进制，要将整数部分和小数部分分别进行转换，这两部分的转换规则是不同的。

整数部分的转换

整数部分的转换规则为：反复除以基数R，直到余数为0为止，每次除法得到的余数从下到上依次排列即是R进制数最终结果。

我们看一个例子，将十进制数135分别转换成八进制数和二进制数：

所以135(D) = 207(O) = 10000111(B)。

小数部分的转换

小数部分的转换规则为：要转换的十进制数乘以基数R，得到的数字小数部分继续与基数R相乘，直到某一步结果的小数部分为0为止。每次相乘得到的中间结果从高到低依次排列即是最终结果。

例如将十进制小数0.6875分别转换成二进制数和八进制数：

0.6875 * 2 = 1.375  整数部分=1  （高位）
0.735 * 2 = 0.75    整数部分=0    ↓
0.75 * 2 = 1.5      整数部分=1    ↓
0.5 * 2 = 1.0       整数部分=1  （低位）

所以0.6875(D) = 0.1011(B)。

1 2	0.6875 * 8 = 5.5 整数部分=5 （高位） 0.5 * 8 = 4.0 整数部分=4 （低位）

所以0.6875(D) = 0.54(O)。

有一种情况就是每次乘积后的小数部分永远得不到0，这种情况下得到的是个近似值。

例如将十进制小数0.63转换成二进制数：

0.63 * 2 = 1.26     整数部分=1  （高位）
0.25 * 2 = 0.52     整数部分=0
0.52 * 2 = 1.04     整数部分=1
0.04 * 2 = 0.08     整数部分=0  （低位）
...

所以0.63(D) = 0.1010…(B)。

含整数、小数部分的转换

我们知道了整数部分和小数部分的转换规则，对一个数字这两部分分别转换，再这两部分转换的结果合起来就得到一个完整的结果。

那么135.6875分别转换成二进制数和八进制数的结果为：

1	135.6875(D) = 10000111.1011(B) = 207.54(O)

二进制、八进制、十进制互相转换

八进制数转二进制数

八进制数转换成二进制数，只需要把每一个八进制数逐位改成等值的3位二进制数即可。

在上图各进制数值之间的对应关系得知，八进制数与二进制数对应关系如下：

1 2	0(O) = 000 1(O) = 001 2(O) = 010 3(O) = 011 4(O) = 100 5(O) = 101 6(O) = 110 7(O) = 111

将八进制数13.724转换成二进制：

1	13.724(O) = 001 011.111 010 100(B) = 1011.1110101(B)

十六进制数转二进制数

十六进制数转换二进制数方法与上面类似，只需要把每一个十六进制数逐位改写等值的4位二进制数即可。

十六进制数与二进制数对应关系如下：

0(H) = 0000  1(H) = 0001  2(H) = 0010  3(H) = 0011
4(H) = 0100  5(H) = 0101  6(H) = 0110  7(H) = 0111
8(H) = 1000  9(H) = 1001  A(H) = 1010  B(H) = 1011
C(H) = 1100  D(H) = 1101  E(H) = 1110  F(H) = 1111

将十六进制数2B.53转换成二进制：

1	2B.5E(H) = 0010 1011.0101 1110(B) = 101011.0101111(B)

二进制数转八进制数

二进制数转换为八进制数，正好与上面相反：整数部分从低位到高位方向每3位改写成八进制数替换，最后不足3位时在高位补0凑满3位。小数部分从高位向低位方向每3位改写成八进制数替换，最后不足3位时在低位补0凑满3位。

例如：

1 2	0.10101(B) = 000.101 010(B) = 0.52(O) 10011.01(B) = 010 011.010(B) = 23.2(O)

二进制数转十六进制数

二进制数转换为十六进制数与上面类似，只不过是每4位改写成十六进制数替换。

例如：

1	11001.11(B) = 0001 1001.1100(B) = 19.C(H)

以上可以看出，二进制与八进制、二进制与十六进制之间的转换关系非常直观，通过简单的规则直接替换即可。

由于二进制数太长，书写和阅读步方便，所以在程序开发或阅读机器代码时，一般采用八进制或十六进制等价表示二进制。

Kaito's Blog

计算机系统基础（二）数值进制和进制转换