我们知道计算机中数字都是使用的二进制表示和运算,对于我们熟悉的十进制数字,可以通过数值进制公式进行转换后计算和显示。
但除了这种编码方式之外,计算机有时为了显示和计算方便,对十进制还定义了新的编码方式:ASCII码字符表示、BCD码表示。这篇文章我们来了解一下这2种编码方式的特点。
ASCCI码字符表示
如果只是对十进制数进行打印或显示,那么可以把十进制数看成字符串,直接用ASCII码表示,09分别对应ASCII码的30H39H,这种表示方式,1位十进制用8位二进制数表示。
用ASCII码表示的十进制又分为前分隔数字串和后嵌入数字串。
前分隔数字串
前分隔数字串将符号位单独用一个字节表示,放在数字串之前。
正号(+)用ASCII码2B(H)表示,符号(-)用2D(H)表示。
例如十进制数+236用前分隔数字串表示为0010 1011 0011 0010 0011 0011 0011 0110,对应的十六进制为2B 32 33 36,在内存中占用4个字节。
十进制数-2369用前分隔数字串表示为0010 1101 0011 0010 0011 0011 0011 0110 0011 1001,对应的十六进制为2D 32 33 36 39,在内存中占用5个字节。
可见,十进制数每增加一位,就要多一个字节表示对应数字。
后嵌入数字串
后嵌入数字串的符号位不单独用一个字节表示,而是嵌入到最低一位数字的ASCII码中。
正数的最低一位数字编码不变,负数的最低一位数字编码的高4位由原来的0011变为0111。
同样是上面2个数字,+236用后嵌入数字串方式表示为0011 0010 0011 0011 0011 0110,对应的十六进制为32 33 36,在内存中占用3个字节。
十进制-2369用后嵌入数字串方式表示为0011 0010 0011 0011 0011 0110 0111 1001,对应的十六进制为32 33 36 79,在内存中占用4个字节。
后嵌入数字串方式比前分隔数字串方式少占用一个字节,但对于负数来说,最低一位数字不是采用十进制数字的ASCII码,所以在显示或打印前必须先转换成可打印字符编码。
用ASCII码表示十进制是为了方便十进制数的输入和输出,但这种方式对于十进制数的计算很不方便。如果要对这种十进制数字进行计算,则必须要转换成二进制数或用BCD码表示十进制了。
BCD码表示
在数据输入输出量很大的商用领域,由于涉及到非常多的十进制数字计算,如果每次都要转换为二进制计算,再转换回十进制显示,那么这之间会对硬件的运算造成较大压力。如何解决这个问题,BCD码就是一种解决大量十进制数输入、输出、运算的场景的一种编码方式。计算机中可用专门的逻辑线路对BCD码进行计算。
十进制0~9共10个数字,因此可用4位二进制位表示即可。4位二进制位可以组合出16种状态,所以从16种状态中选取10种状态就可以表示十进制数,并且可以产生多种BCD码。
BCD码又分为有权BCD码和无权BCD码。
有权BCD码
有权码是指表示每个十进制数位的4个二进制位,都有一个确定的权,以下是常用的几种有权码方案:
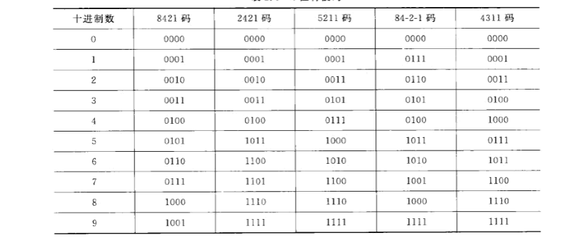
其中最常用的编码是842码,它选取4位二进制数并按顺序取前10个代码与十进制数字对应,每位权从左到右分贝为8、4、2、1,因此称为8421码。
无权BCD码
与有权码相对应,每个十进制位没有确定的权,这种编码叫做无权码。
无权码方案中用的较多的是余3码和格码:
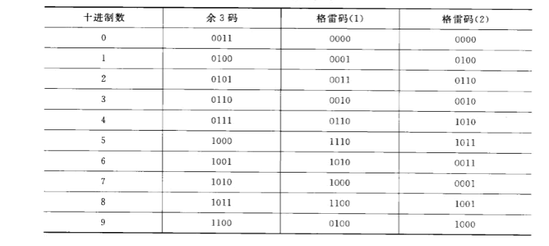
余3码是在8421码的基础上,把每个代码都加0011形成的,优点是执行十进制数加法时,能正确进位,且减法运算提供便利。
格雷码规则是任何两个相邻的代码只有一个二进制位的状态不同,其余3个二进制必须相同,这样设计的好处在于从一个编码变到下一个编码试,只有一位发生变化,变码速度最快,利于电路的设计和运行。
使用BCD码会耗费更多的设备量,所以通常情况下,计算机内部一般使用二进制数进行数据的表示和运算。
总结
我们总结十进制数的编码方案:
- 十进制数字除了用数值进制转换编码外,还可以用ASCII码和BCD码进行编码和运算
- ASCII码一般用于输入和输出的表示,转换位数一一对应,简单直观
- BCD码则用于大量商业运算领域,减少十进制和二进制大量转换而提出的编码方案
- 计算机内部一般还是使用二进制数对数据进行表示和运算,我们对十进制数的编码方案了解即可

